Kysymyksenasettelu tutkimuksessa ja tulosten tulkinta
Tutkimuksen kysymyksenasettelun merkitys on tutkimusta tehtäessä keskeinen, sillä meillä on mahdollisuus saada ainoastaan ja vain sellaisia vastauksia, mitä osaamme ja ymmärrämme kysyä. Kuten Mellin (2006, 240) huomauttaa, että jos tilastollisen tutkimuksen kohteena olevaan ilmiöön liittyy enemmän kuin yksi muuttua, ei yhden muuttujan tilastolliset menetelmät anna laaja-alaista kuvaa ilmiöstä. Merkittävin osa tilastotiedettä käsittelee yleensä kahden tai useamman muuttujan välisten riippuvuuksien kuvaamista ja mallintamista. Mellin (2006, 240) tarkastelee teoksessaan vain kahden muuttujan välisiä riippuvuuksia, koska muuttujien välinen riippuvuus on eksaktia, mikäli toisen arvot voidaan ennustaa tarkasti toisen saaminen arvojen perusteella. Muuttujien välinen riippuvuus on niissä tapauksissa tilastollista, mikäli sanottujen muuttujien välillä ei ole eksaktia riippuvuutta, mutta toisen muuttujan arvoja voidaan kuitenkin käyttää apuna toisen muuttujan arvojen ennustamisessa.
TEKSTI | Margit Mannila
Kun kyseessä on kahden muuttujan välisestä (lineaarisesta) tilastollisesta riippuvuudesta, tätä kutsutaan tilastotieteessä korrelaatioksi. Lineaarisen eli (korrelaation) tilastollisen riippuvuuden voimakkuutta mittaavia tilastollisia tunnuslukuja kutsutaan korrelaatiokertoimeksi. Käytännössä korrelaatiot siis muodostavat perustan muuttujien välisten (lineaaristen) riippuvuuksien ymmärtämiselle. (Mellin 2006, 240.) Käytännössä korrelaatiot muodostavat perustan eri muuttujien välisten riippuvuuksien ymmärtämiselle. Useissa tapauksissa riippuvuuksia tutkitaan (analysoidaan) tarkemmin. Tilastollisista menetelmistä regressioanalyysi on sellainen, jossa niin sanottu selittävän muuttujan tilastollista riippuvuutta joistakin toisista (selittävistä muuttujista) pyritään mallintamaan tilastollisella mallilla, jota kutsutaan regressiomalliksi. (Mellin 2006, 240.) Koska lineaarisessa regressioanalyysissa on tavoitteena selittää jonkin muuttujan vaihtelua yhden tai useamman muuttujan avulla, tulisi näiden olla siis jatkuvia ja lisäksi niiden tulisi olla normaalijakautuneita. Jos on kyseessä ovat kaksiluokkaiset muuttujat, tulisi niiden olla merkattu luvuilla 0 ja 1. (13. Lineaarinen regressioanalyysi.)
Tilastojen tulkinnan ongelmallisuus tulee hyvin esiin esimerkissä, jossa on vertailtu tilastollisesti jäätelön syöntiä ja hukkumiskuolemia. Nopealla vilkaisulla ja selkeällä korrelaatiolla voidaan päätyä johtopäätökseen, että syödyllä jäätelön määrällä ja hukkumisella on vahva korrelaatio.
Käytännössä näin helppoa selitystä hukkumiselle tuskin voidaan antaa, vaikka tilastosta tämä vahva korrelaatio onkin näytettävissä toteen.
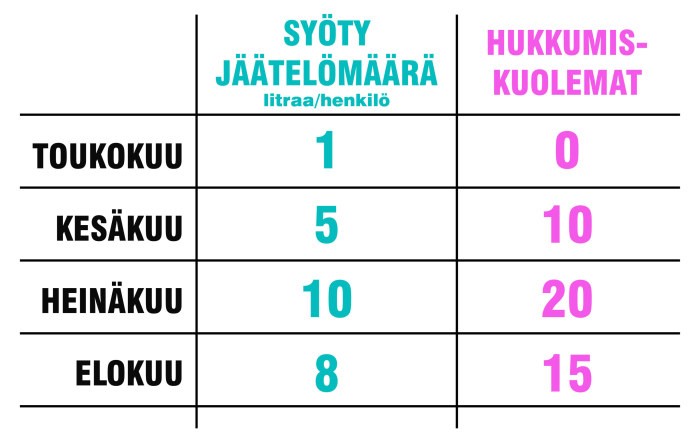
Selittäviä tekijöitä on todennäköisesti muitakin, joten meidän pitäisi tarkastella hieman laajemmin, mikä on todellinen hukkumiskuolemia lisäävä tekijä? Muita syitä, jäätelönsyönnin ohella tai paremminkin sen sijaan, voisivat olla muun muassa lämmin ilma, jolloin ihmiset uivat enemmän kuin kylmällä. Jäätelöä ostetaan myös todennäköisesti enemmän lämpimällä, mutta jäätelö ei ole siis siitä huolimatta hukkumiskuoleminen välitön syy, vaan uiminen on lämpimällä yleisempää ja tästä saattaa olla seurauksena enemmän hukkumiskuolemia. (Heikkinen 2021) On siis syytä olla tarkkana, että ei tehdä aineiston perusteella suoraviivaisia johtopäätöksiä, että ei päädytä vastaavanlaiseen absurdiin johtopäätökseen, että ”jäätelön syönti lisää hukkumiskuolemia”. Vaikka näin ymmärrämme, että väitteenä se olisi absurdi, tapahtuu tällaista tulkintaa tutkimuskontekstissa. Siksi on tärkeää, että tutkimuksen tekijänä kykenet tunnistamaan omasta tutkimuksestasi ”jäätelön”. Se on muuten yllättävän vaikeaa käytännössä.
Johdattelevat kysymykset eivät tuo myöskään hyvää lopputulosta. Esimerkiksi oikeudenkäynnin todistajankuulustelussa johdattelevat kysymykset ovat kiellettyjä. Johdattelevia kysymyksiä tunnistetaan kolme ryhmää. Nämä ovat edellytyskysymykset, odote- eli ehdotuskysymykset sekä epätäydelliset valintakysymykset.
Edellytyskysymys on kysymys, joka perustuu sellaiseen faktoja koskevaan oletukseen, joka ei ole tullut vielä todistajankertomuksessa esiin. Tällaisen faktan voidaan kuitenkin olettaa olevan kuultavana olevan tiedossa. Vastaavasti ehdotuskysymyksessä kysymys on muotoiltu tavalla, josta käy ilmi vastaus, jota kysyjä odottaa. Epätäydellinen valintakysymys puolestaan rajaa vastausmahdollisuuksia, antamatta kuultavalle vapautta valita. Aivan samalla tavalla tutkimuksessakin tutkija voi ohjata tutkittavaa vastaamaan kysymyksiin haluamallaan tavalla tai pyytämällä tutkittavaa vastaamaan epätäydellisiin valintakysymyksiin. (Vuorenpää). Jotta tällaisilta kysymyksiltä vältytään, kannattaa lomake testata tai vähintään pyytää vaikka opiskelukaveria lukemaan lomake. Palauteeksi ei riitä ihan hyvä.
Klassinen esimerkki argumentaatiovirheestä on suljettu valintakysymys, jossa pakotetaan vastaaja valitsemaan kahdesta vaihtoehdosta toinen tai vastaamaan tietyllä tavalla. Tällaisessa tilanteessa kysyttävä kysymys on siis vahvasti arvoväritteisessä (vahva ennakkoasenne) muodossa ja vaihtoehtoina vastukseen on ainoastaan kyllä tai ei. Tällaisesta kysymyksestä käytetään usein esimerkkinä kysymystä: Oletteko jo lopettanut puolisonne hakkaamisen? Koska siis vastausvaihtoehdot ovat vain kyllä tai ei, syntyy molemmissa tapauksissa vaikutelma, että on käyttäytynyt näin tai vastaavasti tekee asiaa yhä edelleen. Suunnitellessasi mittaria (kyselylomake) perehdy huolellisesti millaisella tavalla saat kohdejoukolta juuri sinun tutkimuksesi kannalta merkityksellisen tiedon, jotta voit vastata tutkimustehtävääsi luotettavalla tavalla. (Mannila 2021.)
Kun tutkimuskysymyksiä suunnitellaan, on syytä välttää juuri tämän tapaisia arvoväritteisiä kysymyksiä tai kysymyksiä joihin vastaamiseen antaa vain esimerkiksi vaihtoehdoiksi kyllä tai ei vastauksen.
Esimerkiksi Heikkilä (2014, 152) tiivistää kausaalisuhteen (syy-seuraussuhde) edellytykset neljään kohtaan, jotka ovat: ensinnäkin muuttujien yhteisvaihtelu, toiseksi niiden ajallinen järjestys tulee olla oikea (syy on oltava ennen seurausta), kolmanneksi seuraus ei aiheudu kolmannesta, ulkopuolisesta tekijästä, joka on yhteinen syy molemmille tarkasteltaville muuttujille tai neljänneksi teoria tukee tulkintaa. Korrelaatiokertoimen tulkintavirheitä voivat aiheuttaa seuraavat neljä tekijää. Ensinnäkin muuttujien välillä voi olla epäsuora riippuvuus (esimerkiksi edellä mainittu kolmas muuttuja). Toiseksi muuttujien välinen riippuvuus ei ole lineaarinen. (Katso Mellin 2006). Kolmanneksi haasteita aiheuttavat poikkeavat havainnot (outliers), jotka herkästi muuttavat kertoimen arvoa (tutki näitä hajontakaaviolla) ja neljäntenä on autokorrelaatio (muuttujan arvoon vaikuttaa yksi tai useampi edeltävä arvo), joka on yleinen varsinkin aikasarjoissa. Autokorrelaation tunnistaminen saattaa mennä täysin ohi aloittelevalta ja vähän kokeneemmaltakin tutkijalta tulosten tulkintavaiheessa.
Lopuksi
Huomattavan moni ensimmäistä tutkimusta tekevä haluaa tutkija jonkin asian vaikuttavuutta johonkin toiseen asiaan. Yleensä tekijällä on tästä varsin vahva ennakkokäsitys ja hän luottaa vaikuttavuuteen ja sen ihmeitä tekevään voimaan nimenomaisen kysymyksen ratkaisuavaimena. Alkula, Pötinen & Ylöstalo (2002, 200) huomauttavat, että selittävän analyysin peruslähtökohtana on tilanne, jossa halutaan osoittaa muuttujan x vaikuttavan muuttujaan y, on näiden muuttujien yhteisvaihtelu välttämätön, mutta ei riittävä ehto, kuten edellä esitetty esimerkki jäätelönsyömisen ja hukkumistapausten välillä osoittaa.
Kun siis on tehty kahden muuttujan taulukko ja tutkija haluaa edetä kausaalipäätelmiin, syntyy tilanne, jossa elaboraatio saattaa osoittautua hyödylliseksi. Toisin sanoen, kun aluksi on tutkittu kahden muuttujan välistä yhteisvaihtelua (x ja y, joista toinen voi puuttua ja toinen toteutua/olla). Tähän vakioidaan kolmas muuttuja. Kutsutaan sitä muuttujaksi z. Asetelma muuttuu siten, että tutkitaan x:n ja y:n yhteisvaihtelua z:n luokissa edelleen. Havaitaan että alkuperäinen yhteys joko säilyy ennallaan tai sitten se muuttuu alkuperäisestä joko vahvistuen tai heikentyen tai sitten se häviää kokonaan. Se on kuitenkin samanlainen kaikissa z:n luokissa tai sitten se on alkuperäisestä poikkeava ja erilainen z:n luokissa. (Alkula ym. 2002, 200201.) Suosittelen vahvasti tutustumaan elaboraatioon tarkemmin, sillä tässä asiaa käsiteltiin pienenä pintaraapaisuna.
-
13. Lineaarinen regressioanalyysi. Viitattu 17.12.2021. https://www.tutkijaportti.fi/wp-content/uploads/sites/17/2021/05/13-Lineaarinen-regressioanalyysi.pdf
-
Alkula, T., Pöntinen, S. & Ylöstalo, P. 2002. 1.─4. painos. Sosiaalitutkimuksen kvantitatiiviset menetelmät. WSOY. Helsinki.
-
Heikkinen, S. 2021. Jäätelö lisää hukkumiskuolemia – vai miten se menikään? Vältä nämä tilastojen tulkinnan kompastuskivet. Oppiminen. Yle.fi. Viitattu 23.11.2021 https://yle.fi/aihe/artikkeli/2021/03/27/jaatelo-lisaa-hukkumiskuolemia-vai-miten-se-menikaan-valta-nama-tilastojen
-
Heikkilä, T. 2014. Tilastollinen tutkimus. Edita Publishing. Viitattu 17.12.2021. http://www.tilastollinentutkimus.fi/1.TUTKIMUSTUKI/KvantitatiivinenTutkimus.pdf
-
Mellin, I. 2006. Tilastolliset menetelmät. Lineaarinen regressioanalyysi. Aalto. Viitattu 17.12.2021. https://math.aalto.fi/opetus/sovtoda/oppikirja/Regranal.pdf
-
Mannila, M. 2021. Quantitative Research – Types of Measurement Scales. Energiaa. Vaasan ammattikorkeakoulu. Viitattu 17.12.2021. https://energiaa.vamk.fi/en/komptence/quantitative-research-types-of-measurement-scales/
-
Vuorenpää, M. Todistajankuulustelu. Tieteen termipankki. Viitattu 23.11.2021. https://tieteentermipankki.fi/wiki/Oikeustiede:todistajankuulustelu
Comments